出稿金額ごとのリーチ率、「なんとなく」で想像していませんか?
事業会社やスタートアップなどで広告運用を任されたとき、
「TVっていくら出せば何%くらい届くの?」
「YouTubeとXならどちらが費用対効果が良さそう?」
といった感覚的な問いに、答えを出せずに困ったことはありませんか?
実はこれ、広告代理店の現場でも得意先から非常によく聞かれる質問です。
そこで今回は、媒体ごとのリーチ率を簡易的に予測するための方法と、Pythonを使った自動計算の仕組みをご紹介します。
本記事でできること
- 媒体別の「出稿金額×リーチ率」データ(参考値)の確認
- Pythonコードをコピペするだけで「成長曲線(サチュレーション)」を自動推定
- Excelに出力し、1円あたりのリーチ効率を予測できるシミュレーターを自作できる
各媒体の出稿金額に対するリーチ率(参考表)
以下は、過去の広告実績データ(ノーム値)をもとに作成した参考値です。
下のダウンロードボタンからcsvファイルをダウンロードして活用ください!
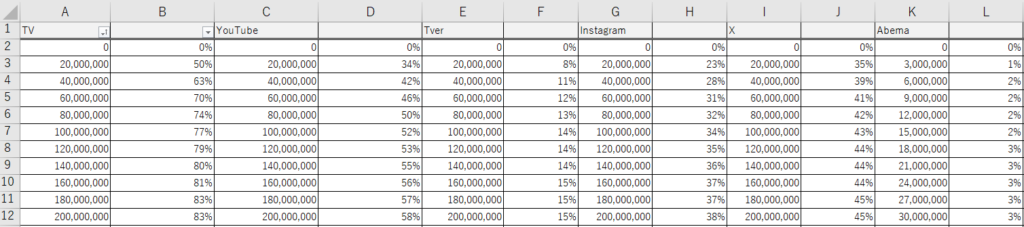

そのまま実務レベルで活用できるくらいデータ精度が高いデータをご用意しました。
今回使う媒体は「TV/YouTube/TVer/Instagram/X/Abema」6媒体ですが、出稿金額に比例してリーチ率が単純に伸びるわけではない点がポイントです。
媒体ごとに“効率が鈍化する地点”があり、そこを把握することが合理的な予算配分につながります。
このExcelをPythonに読み込ませると、1円あたりのリーチ効率まで見える!
ここからが本題です。
先ほどのExcelファイルだけでは、2,000万円単位のリーチ率しか分からず、かなりアバウトな効果しか把握できないのが課題です。
しかし!
先ほどのExcelファイルを、以下のPythonコードに読み込ませて実行するだけで…
- 各媒体のリーチ成長曲線が自動的に計算され、
- 「a」「b」「最大値K」「x桁」「y桁」「決定係数R²」などが出力されます
- これらを使って、1円あたりのリーチ率まで算出可能なExcelシミュレーターが完成します
少し難しそうに見えるかもですが、次に紹介するPythonコードをコピペするだけで誰でも簡単に実現できます。
コピペで使えるPythonコード全文(Colab推奨)
※Pythonの環境がお手元に整っていない場合はこちらを参考にサクッと環境を整えましょう。
【超初心者向け】5秒でできるPython環境構築ガイド【Google Colab編】
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit
from sklearn.metrics import r2_score # 決定係数計算用
# 近似モデル式の関数(サチュレーションを考慮)
def func_fit(x, a, b, K):
# サチュレーションを考慮し、Kに最大値(例: 100)を設定
K = min(K, 100) # Kが100を超えないようにする
y = K / (1 + (a * x ** b))
return y
#データの読み込み(今回はexcel)
df = pd.read_excel('input.xlsx', sheet_name='A_入力')
num = int(df.shape[1]/2) # 目的変数の数
df
# Fitting
for i in range(num):
df_temp = pd.DataFrame()
df_temp = df.iloc[:,[i*2,i*2+1]]
df_temp.dropna()
df_temp
name_list = []
a_list = []
b_list = []
K_list = []
R_list = []
d_x_list = []
d_y_list = []
max_fev=100000000
df2 = pd.DataFrame()
for i in range(num):
df_temp = pd.DataFrame()
df_temp = df.iloc[:,[i*2,i*2+1]]
df_temp = df_temp.dropna()
x_observed = df_temp.iloc[:,0]
y = df_temp.iloc[:,1]
# 説明変数と目的変数の桁数を数える
max_num = max(x_observed)
s_x = str(max_num)
if '.' in s_x:
s_x_i, s_x_d = s_x.split('.')
else:
s_x_i = s_x
s_x_d = '0'
d_x = float(len(s_x_i))
max_num = max(y)
s_y = str(max_num)
s_y_i, s_y_d = s_y.split('.')
d_y = float(len(s_y_i))
# スケール調整
x_observed = x_observed / 10**d_x
y = y / 10**d_y
max_num = max(y)*10
# 境界条件 (Kの最大値を100にする)
bounds = ((0,-5,0), (100, 0, min(max_num, 100)))
name = df.columns.values[i*2]
param, pcov = curve_fit(func_fit, x_observed, y, bounds=bounds, maxfev=max_fev)
fit_y = func_fit(x_observed, param[0], param[1], param[2])
# スケールを戻して保存
df2[name+"_x"] = x_observed * 10**d_x
df2[name+"_y"] = y * 10**d_y
df2[name+"_fit"] = fit_y * 10**d_y
# R2スコアの計算
R2 = r2_score(fit_y, y)
# パラメータのリスト保存
name_list.append(name)
a_list.append(param[0])
b_list.append(param[1])
K_list.append(param[2])
d_x_list.append(d_x)
d_y_list.append(d_y)
R_list.append(R2)
# パラメータをDataFrameにまとめる
df_param = pd.DataFrame({
"name": name_list,
"a": a_list,
"b": b_list,
"max_value": K_list,
"d_x": d_x_list,
"d_y": d_y_list,
"Number of decisions": R_list
})
# 結果をExcelファイルに書き出し
with pd.ExcelWriter("output.xlsx") as writer:
df_param.to_excel(writer, sheet_name='param')
df2.to_excel(writer, sheet_name='data')
✅このコードがやっていること(簡単な解説)
- Excelの各媒体列(出稿金額とリーチ率)を読み込み
- Pythonで“リーチ成長曲線”を自動でフィッティング
- パラメータ(a, b, K)とスケーリング桁数(x, y)を抽出
- それらをExcelに出力し、誰でも再利用できるようにする
なお、上記について詳しく知りたい人は以下をご参照ください!
なぜ”リーチ成長曲線”なの??
広告のリーチ率(どれだけの人に届いたか)は、出稿金額が増えるにつれて以下のような特性を示します:
- 初期は急激に増加(低予算でもよく届く)
- 徐々に増加が鈍化(似た層に何度も届いて新規が減る)
- 限界(最大値K)に近づいていく
この「成長→鈍化→頭打ち」のパターンを捉えるために使われるのが、S字型の非線形モデル(ロジスティック型)です。
統計学的に使っているモデル
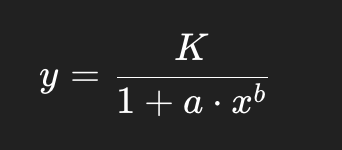
▶ このモデルの特徴と解釈
| 要素 | 解釈 |
| K | リーチ率の理論的上限(例:100%) |
| a | 曲線の傾きの制御(大きいと立ち上がりが急) |
| b | 鈍化のカーブ度合い(0に近いとリニアに近くなる) |
| xb | 指数的な変化を与えることで“鈍化”を表現 |
この式は、シグモイド(S字)型のロジスティック成長関数のバリエーションであり、
マーケティングでは「媒体効果の限界」や「消費の飽和」などを表現するのに非常によく使われます。
Pythonでの”フィッティング”とは??
フィッティングとは:
実際に観測されたデータ(出稿金額とリーチ率)に、
上記の関数モデルを最もよく当てはまるように調整する処理のこと
▶ 使用している関数
from scipy.optimize import curve_fit
これは「非線形最小二乗法」という手法で、
- モデル式 y=K/(1+a⋅xb)に対して
- 各点の誤差(残差)を最小化するように
- a,b,Kの最適な値を自動的に見つけます
なぜこのモデルが使いやすいの??
✅ データ点が少なくてもフィットしやすい(3パラメータモデル)
✅ 曲線の「鈍化」「限界到達」「差分効率」を直感的に把握できる
✅ Excel関数で再現可能 → 非エンジニアにとっても展開しやすい
Excelで1円あたりのリーチ率を算出する方法
Pythonが出力したExcelファイル内には、以下のようなパラメータが含まれています。
a,b,K:成長曲線の係数x桁,y桁:元データのスケーリング調整用R²:精度を示す決定係数
これを使えば、Excel上で以下の式を入力するだけで、任意の出稿金額に対するリーチ率を即座に計算できます:
=K/(1 + a * (出稿金額 / 10^x桁)^b) * 10^y桁
📌Excelの計算例
例えば、以下のようなExcelファイルを作ると非常に分かりやすくなります。

そして、例えばTVに1,000万円投下した時のリーチ率(C14セル)を計算式は添付の通りです。
※冒頭でダウンロードしたExcelファイルとは、記載媒体が異なっている点ご容赦ください。
これで、任意の出稿金額に対する想定リーチ率が簡単に算出できるようになりました!
まとめ|「感覚」ではなく、「根拠」でメディア予算を組もう
この記事で紹介した手順を使えば:
- ✅ ざっくりした表でも精度の高い参考モデルが作れる
- ✅ PythonのコードはコピペだけでOK
- ✅ Excel上で誰でも再現可能なシミュレーターに変換できる
媒体の選定に迷ったら、まずは「リーチ効率の見える化」から始めてみてください。



コメント